Parabolic variational inequality
By utilizing a symmetric dual-wind DG (DWDG) spatial discretization and a backward Euler temporal discretization, we proposed a fully discrete scheme designed to solve a parabolic variational inequality. We also determined the rate of convergence of the error in space and time in suitable norms.

Let $\Omega$ be a bounded convex polygonal domain in $\mathbb{R}^2$, $T_F > 0$, and set $J = [0, T_F]$.
For a given $f \in C(J; L^\infty(\Omega))$ and $\psi \in H^1(\Omega)$ with $\psi \leq 0$ a.e. on $\partial \Omega$, we consider the parabolic variational inequality (VI):
For all $t \in (0,T_F]$, find $u(t) \in K$ contained in $H^1_{0}(\Omega)$ such that
\[\begin{array}{rrlrrllll} & ( \partial_t u, v-u ) + a(u, v-u) & \geq & ( f(t), v-u ) & \forall & v \in K \\ & u(0) & = & u_0 \end{array}\]where $u_0 \in K$ is the given initial condition, $K$ is the constrained set with
\[\begin{array}{rrc} & K & := & \{v \in H^1_0(\Omega): v \geq \psi \ \text{a.e. in} \ \Omega\} \end{array}\]and the bilinear forms $(\cdot, \cdot)$ and $a(\cdot, \cdot)$ are defined by
\[\begin{array}{rrcccr} & (v, w) & = & \displaystyle \int_{\Omega} v \, w \, dx \,; & a(v,w) & = & \displaystyle \int_{\Omega} \nabla v \cdot \nabla w \, dx & \forall \, v, w \in H^1(\Omega) \end{array}\]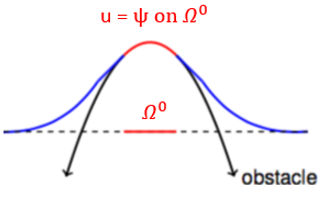
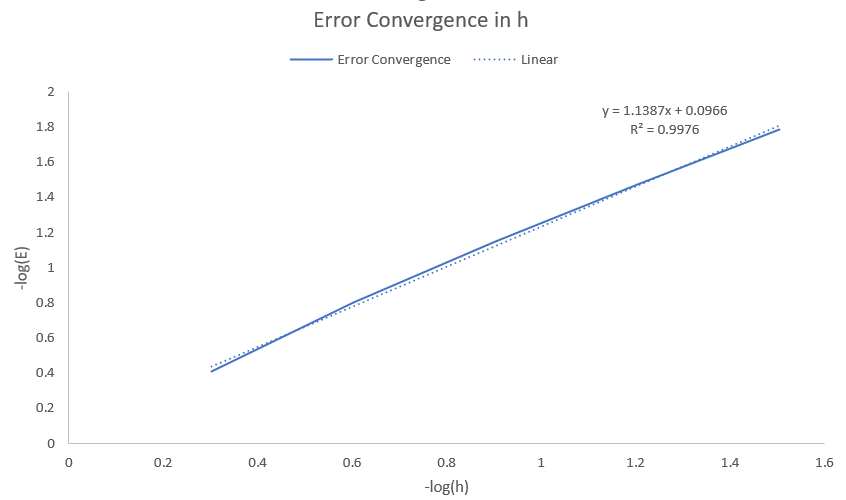
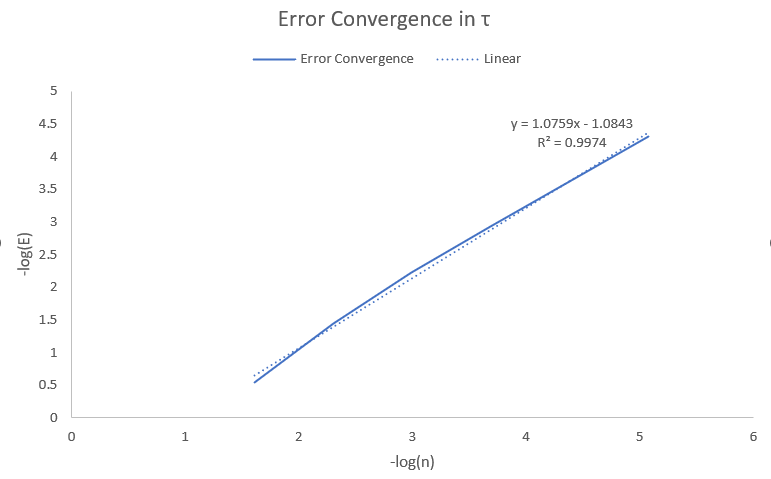
By utilizing a symmetric dual-wind DG (DWDG) spatial discretization and a backward Euler temporal discretization, we propose a fully discrete scheme designed to solve the above time-dependent VI. In this paper, these methods were used to analyze elliptic VIs and sharp error estimates for linear and quadratic elements were derived. Parabolic VIs can be considered as a generalization of elliptic VIs. However, the analysis of these methods in the case of parabolic VIs is more subtle and delicate due to the use of discrete gradient operators and the low regularity of the time derivative $\partial_t u$. We show that the numerical solution tends to converge in $L^\infty(L^2)$ and $L^2(H^1)$-like energy norms as long as the exact solution meets certain regularity conditions. To make the convergence analysis easier, we introduce a novel interpolation operator that combines the standard interpolation operator with a positive-preserving interpolation operator. We then show that the proposed method converges in space and time by $O(h + \tau^{\frac34}(log(\tau^{-1}))^{\frac14})$ in the suitable norm. Under strong assumptions (which are practical*), we improve the order of convergence to $O(h + \tau(log(\tau^{-1}))^{\frac12})$ (see the error convergence in $\tau$ figure below).
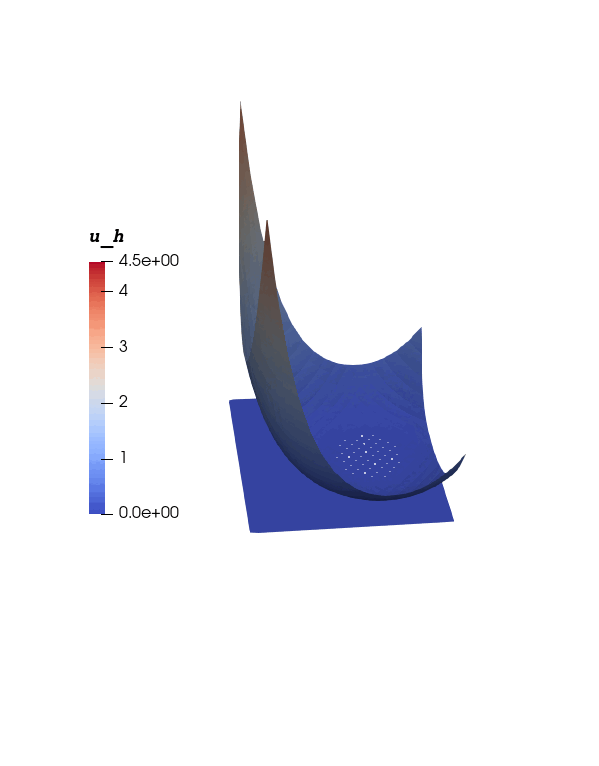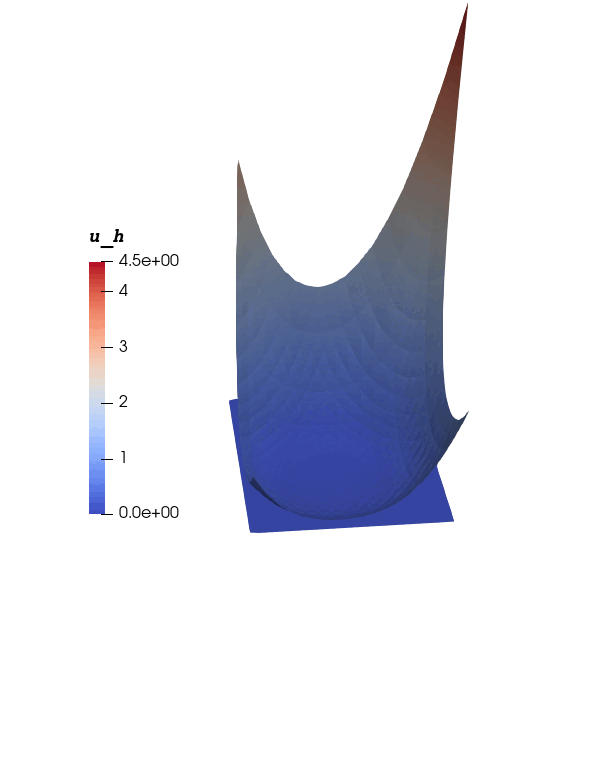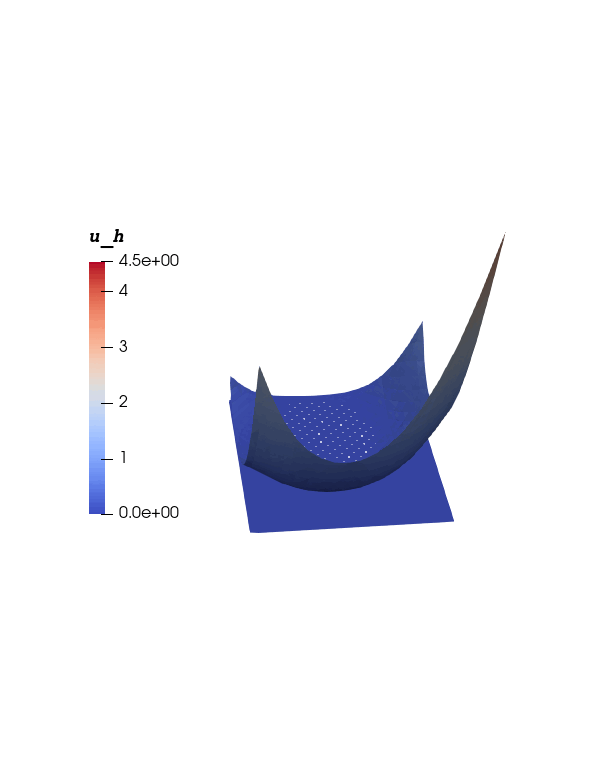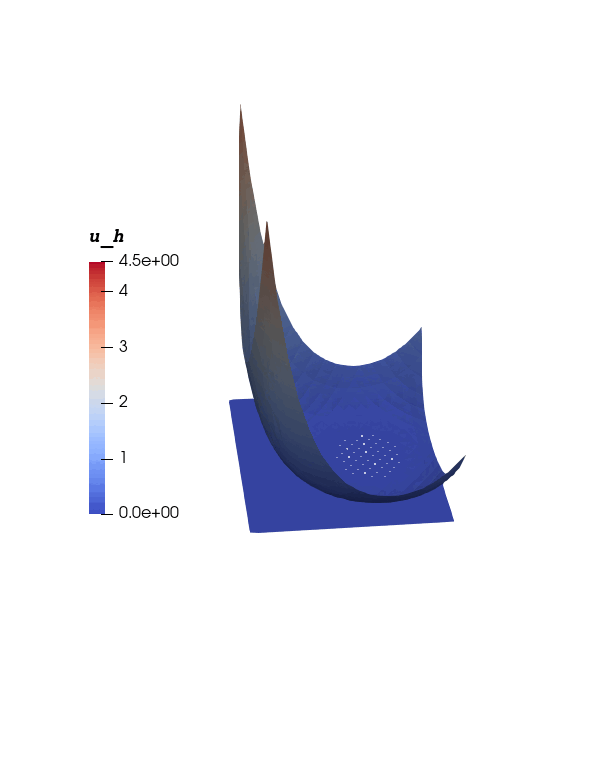
Numerical Experiment - 1: Zero Obstable Problem
[P Majumder 2020]
\(\Omega = [-1,1]^2, \, J=[0,1], \, \psi = 0, \, r_1 = \frac{1}{3}, \, \omega = 4 \\ r_0(t) = \frac13 + 0.3 \sin(4 \omega \pi t), \, c(t) = r_1 ( \cos(\omega \pi t), \sin(\omega \pi t))\)
Contact set and Non-Contact set:
\(\Omega^0(t) = \{ ||x - c(t) ||_2 \leq r_0(t) \} \\ \Omega^+(t) = \{ || x - c(t) ||_2 > r_0(t) \}\)
Exact solution:
\(u(x,t) = \begin{cases} \displaystyle \frac12 \big( ||x - c(t)||^2_2 - r_0^2(t) \big)^2 &\qquad x \in \Omega^+(t), \\ 0 &\qquad x \in \Omega^0(t). \end{cases}\)
Consequently,
\(f(x, t) = \begin{cases} \displaystyle 4r_0^2(t) - 8 ||x-c(t)||_2^2 -2(||x-c(t)||_2^2 - r_0^2(t)) ((x-c(t)) c'(t) + 4r_0(t) r_0'(t))) & x \in \Omega^+(t), \\ -4 r_0^2 \left( 1 - ||x-c(t)||_2^2 + r_0^2(t) \right) &x \in \Omega^0(t). \end{cases}\)