Steady convection-diffusion equation in the convection dominated regime
We proposed and analyzed a numerically stable and convergent scheme for the convection-diffusion (CD) equation in the convection-dominated regime and derived a local order of convergence of $O(ℎ^{1.5})$ whenever the exact solution is of $𝐻^2(\Omega)$ regularity. The following figures illustrate a comparison between the exact and numerical solution from a particular numerical experiment.
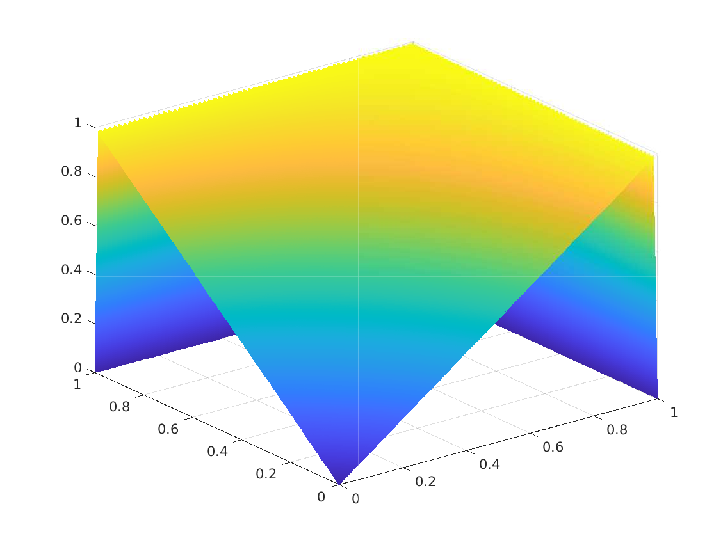
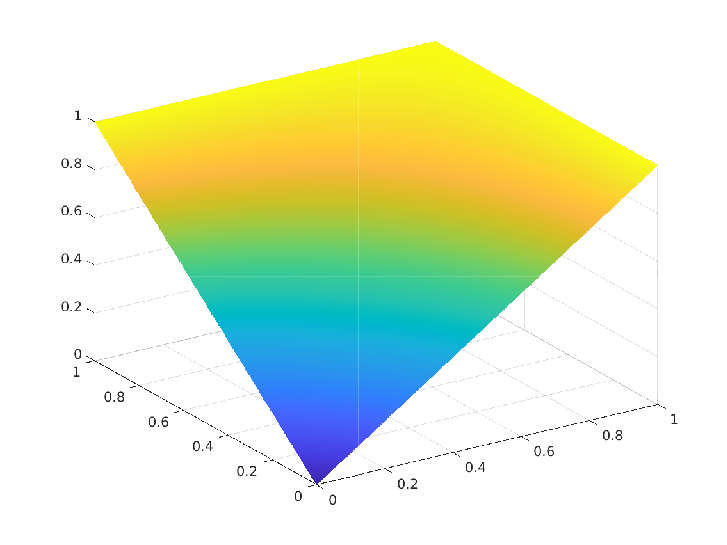
Given a convex polygonal domain $\Omega$ in $\mathbb{R}^2$ with Lipschitz boundary $\partial \Omega$, the convection-diffusion (CD) equation is:
\[\begin{array}{rrcccccccc} & - \epsilon \Delta u + \boldsymbol{\rho} \cdot \nabla u & = & f & \text{in} & \Omega \\ & u & = & g & \text{on} & \partial \Omega \end{array}\]where $\epsilon > 0$ is a constant, $\boldsymbol{\rho}$ is a vector field in $[W^{1,\infty}(\Omega)]^2$, $f \in L_2(\Omega)$ is a given source function and the function $g \in L^{1}(\partial \Omega)$. The unknown scalar function $u$ is some physical quantity that is being transported in the direction $\boldsymbol{\rho}$ along with diffusive effects determined by $\epsilon$. Roughly speaking, $-\epsilon \Delta$ models the diffusion of $u$ while $\boldsymbol{\rho} \cdot \nabla$ models the convection of $u$ in the domain $\Omega$.

In this project, we propose and analyze a numerically stable and convergent scheme for Convection-Diffusion (CD) equation in the convection-dominated regime ($\epsilon \approx 0$). Since the standard CG-FEM for the CD equation causes spurious oscillations, the DG schemes are extremely appropriate for the CD equation. We choose to follow a novel discontinuous Galerkin finite element differential calculus framework and approximate the infinite-dimensional operators in the CD equation by the finite-dimensional operators. Specifically, we construct the numerical method by using the dual-wind DG (DWDG) formulation for the diffusive term and the formulation that uses the average discrete gradient operator for the convective term along with upwinding. We establish the order of convergence of the error assuming the $H^2$ regularity on the exact solution, and provide several numerical tests to demonstrate the theoretical order of convergence of the proposed formulation.
Numerical Experiment - 1: Continuous Solution
\(\Omega = (1,3)^2,\quad \boldsymbol{\rho} = \langle x_1,x_2 \rangle, \quad \epsilon = 10^{-9} \quad u(x_1,x_2) = \dfrac{x_2}{x_1}\)
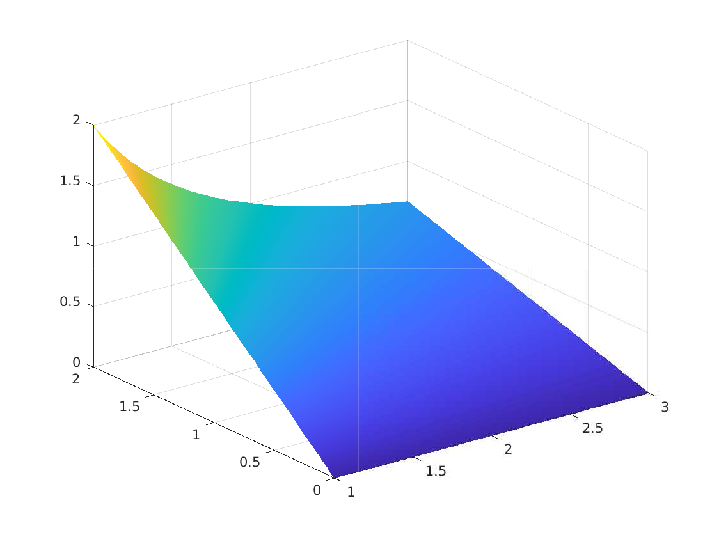
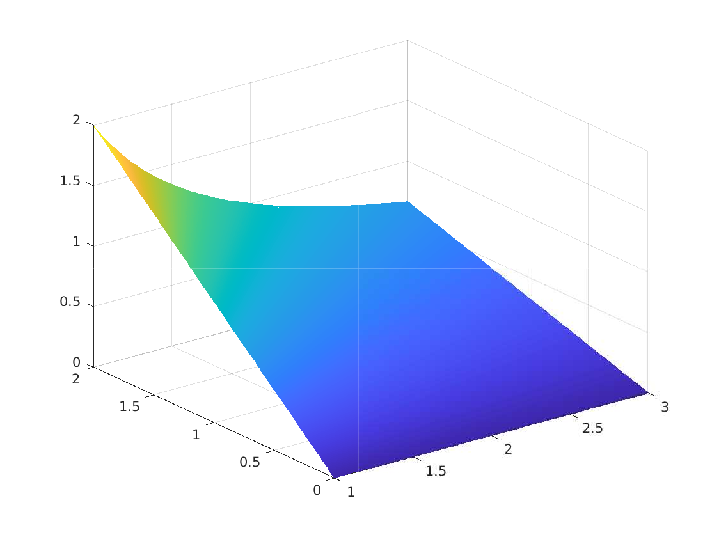
| h | DOF | $L_2$ Error | Rate | $||| \cdot |||$ Error | Rate |
|---|---|---|---|---|---|
| 1/2 | 12 | 1.20e-01 | -- | 2.84e-01 | -- |
| 1/4 | 48 | 4.20e-02 | 1.52 | 9.86e-02 | 1.53 |
| 1/8 | 192 | 9.95e-03 | 2.08 | 3.35e-02 | 1.56 |
| 1/16 | 768 | 2.41e-03 | 2.04 | 1.15e-02 | 1.54 |
| 1/32 | 3072 | 6.01e-04 | 2.01 | 3.97e-03 | 1.53 |
| 1/64 | 12288 | 1.50e-04 | 2.00 | 1.38e-03 | 1.52 |
| 1/128 | 49152 | 3.73e-05 | 2.01 | 4.86e-04 | 1.51 |
Table showing convergence rates in $L_2$ and $||| \cdot |||$ norms.
Numerical Experiment - 2: Boundary Layer
[B Ayuso, LD Marini (2009)]
\(\Omega = (0,1)^2,\quad \boldsymbol{\rho} = \langle 1,1 \rangle, \quad \epsilon = 10^{-9}\) \(u(x_1,x_2) = x_1 + x_2(1-x_1) + \dfrac{\exp \left(\dfrac{-1}{\epsilon} \right)-\exp \left(\dfrac{(x_1-1)(1-x_2)}{\epsilon} \right)}{1-\exp \left(\dfrac{-1}{\epsilon} \right)}\)


| h | DOF | $L_2$ Error | Rate | $||| \cdot |||$ Error | Rate |
|---|---|---|---|---|---|
| 1/16 | 768 | 2.32e-04 | -- | 2.29e-03 | --- |
| 1/32 | 3072 | 5.81e-05 | 2.00 | 8.07e-04 | 1.50 |
| 1/64 | 12288 | 1.43e-05 | 2.00 | 2.85e-04 | 1.50 |
| 1/128 | 49152 | 3.63e-06 | 2.00 | 1.00e-04 | 1.50 |
| 1/256 | 196,610 | 9.08e-07 | 2.00 | 3.56e-05 | 1.50 |
| 1/512 | 786,430 | 2.27e-07 | 2.00 | 1.25e-05 | 1.50 |
Table showing convergence rates in $L_2$ and $||| \cdot |||$ norms. Errors are computed on the subdomain $[0,0.875]^2$