Satyajith (SJ) Bommana Boyana

Satyajith (SJ) Bommana Boyana

Experienced Mechanical Design Engineer, Numerical Analyst, Data Science Enthusiast, and Researcher

Research

My research interests include DG finite element methods, variational inequalities, PDE-constrained optimization, numerical optimization, physics informed machine learning.

Collaborators

Picture of Dr. Yi Zhang
Dr. Yi Zhang (Advisor)
Picture of Dr. Aaron Rapp
Dr. Aaron Rapp
Picture of Dr. Sijing Liu
Dr. Sijing Liu
Picture of Dr. Tom Lewis
Dr. Tom Lewis (Mentor)

Research Projects

Parabolic variational inequality

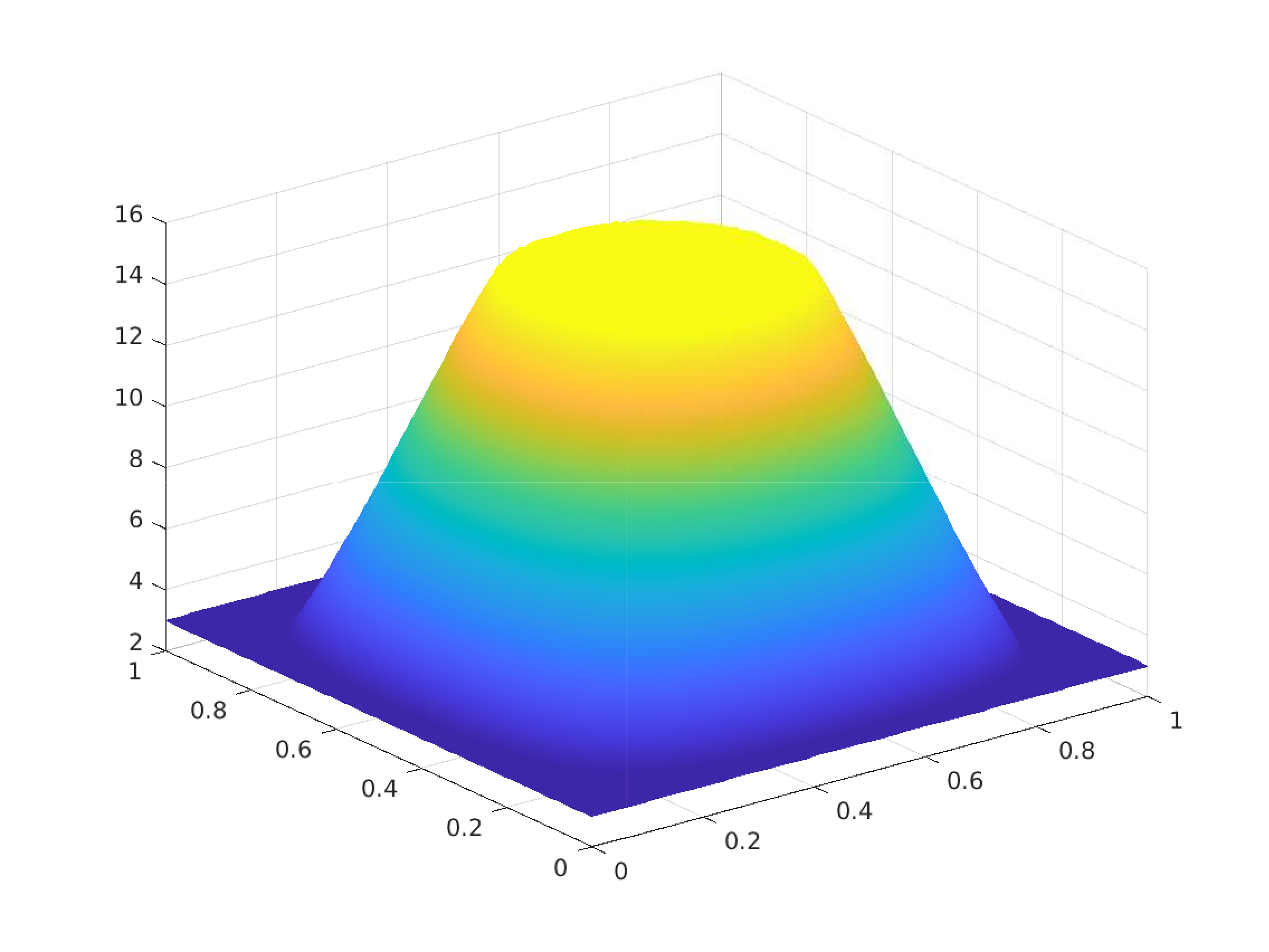
By utilizing a symmetric dual-wind DG (DWDG) spatial discretization and a backward Euler temporal discretization, we proposed a fully discrete scheme designed to solve a parabolic variational inequality. We also determined the rate of convergence of the error in space and time in suitable norms.

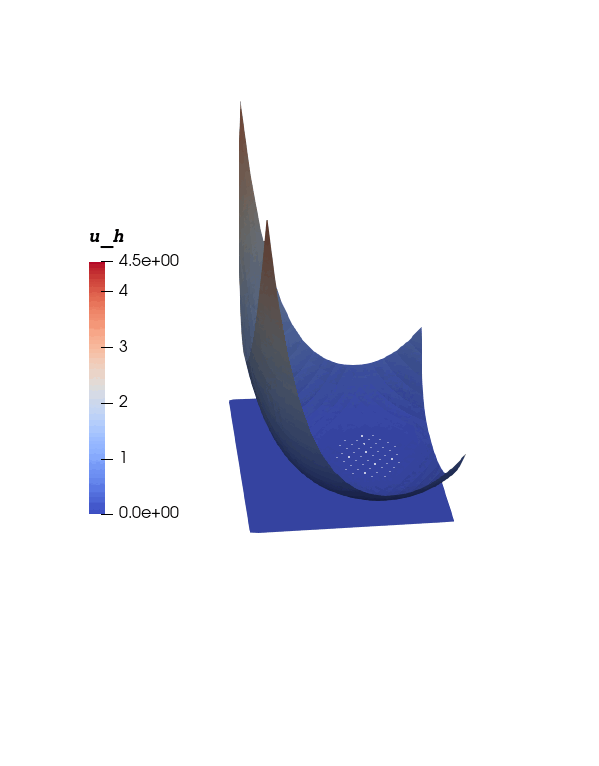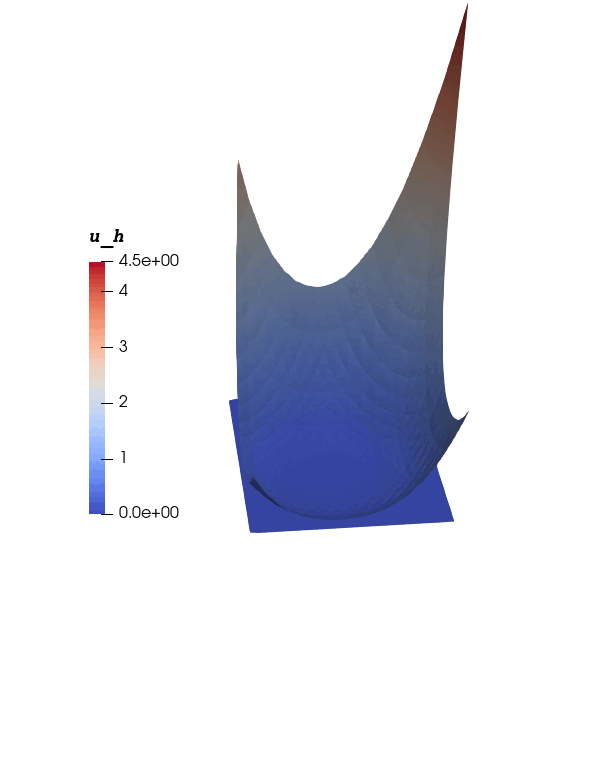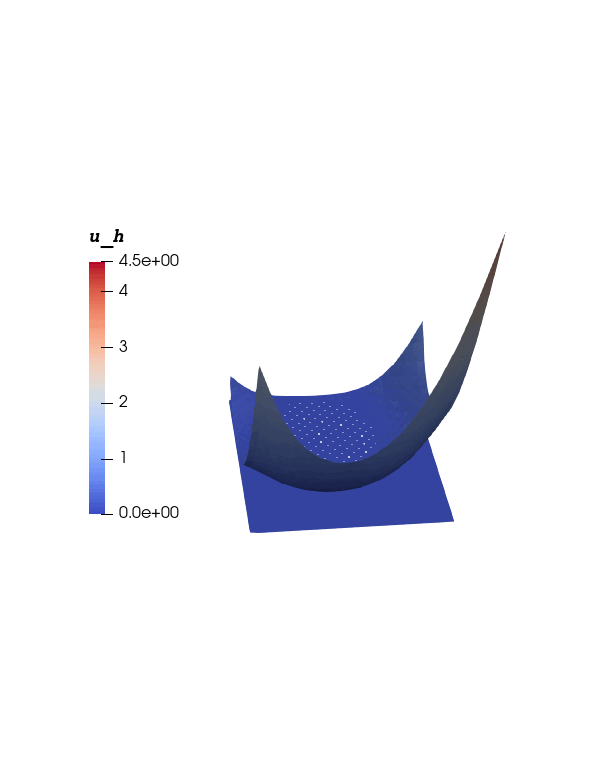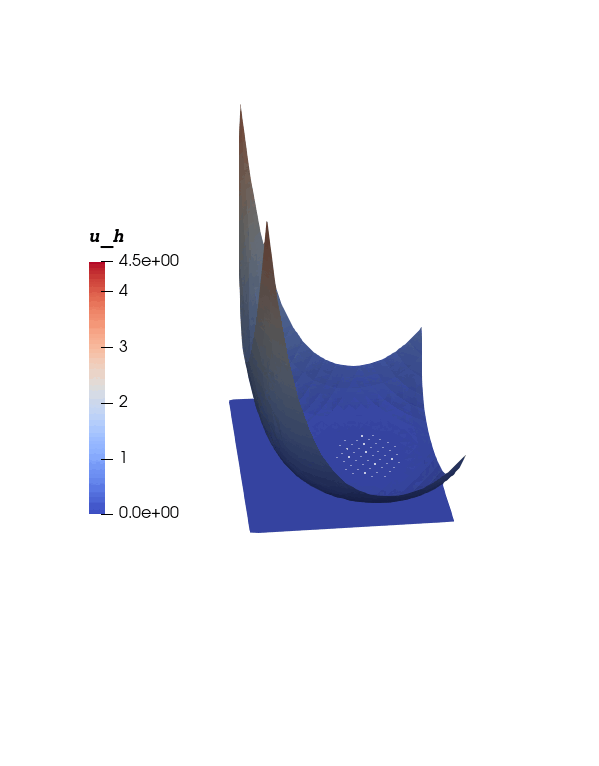Numerical solution for numerical experiment 1: Zero Obstable Problem
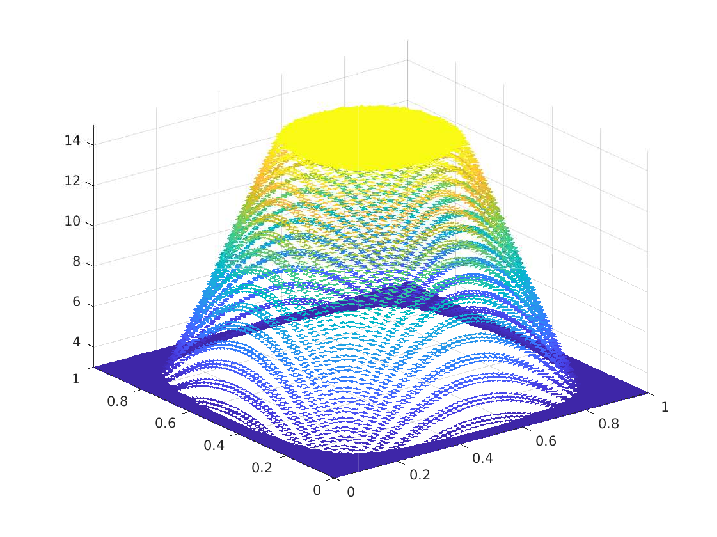
Numerical Solution
Contact sets for numerical experiment 1: Zero Obstable Problem
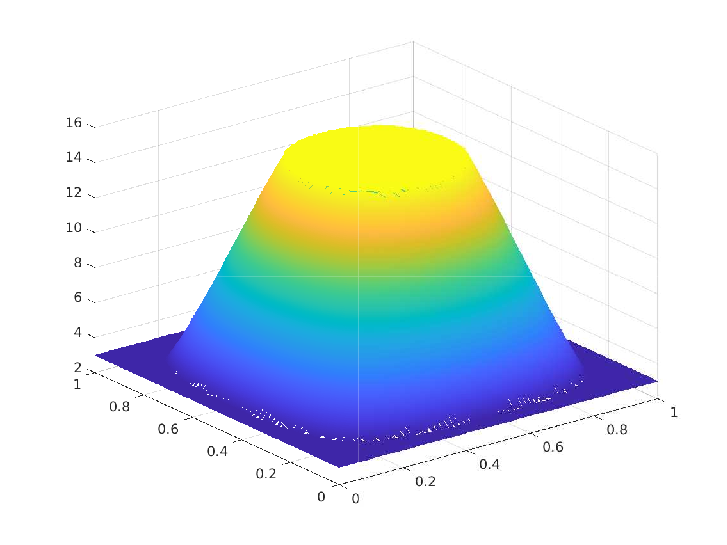
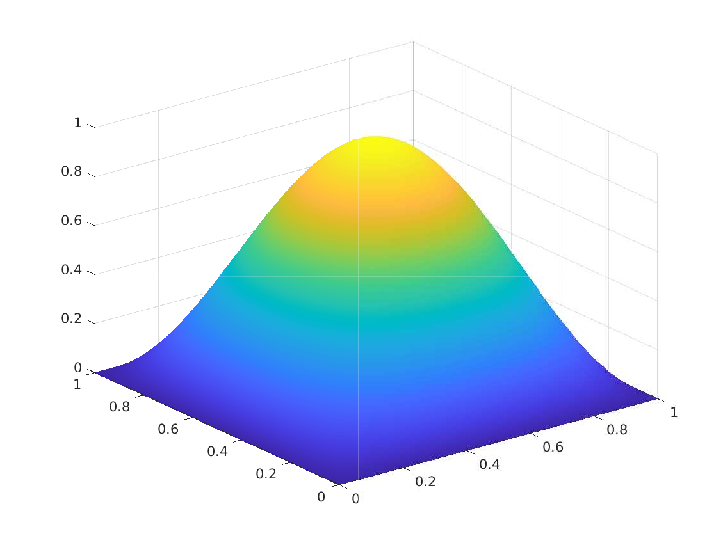
Contact set $\Omega_0(t)$
Read more

Steady convection-diffusion equation in the convection dominated regime

We proposed and analyzed a numerically stable and convergent scheme for the convection-diffusion (CD) equation in the convection-dominated regime and derived a local order of convergence of $O(ℎ^{1.5})$ whenever the exact solution is of $𝐻^2(\Omega)$ regularity. The following figures illustrate a comparison between the exact and numerical solution from a particular numerical experiment.

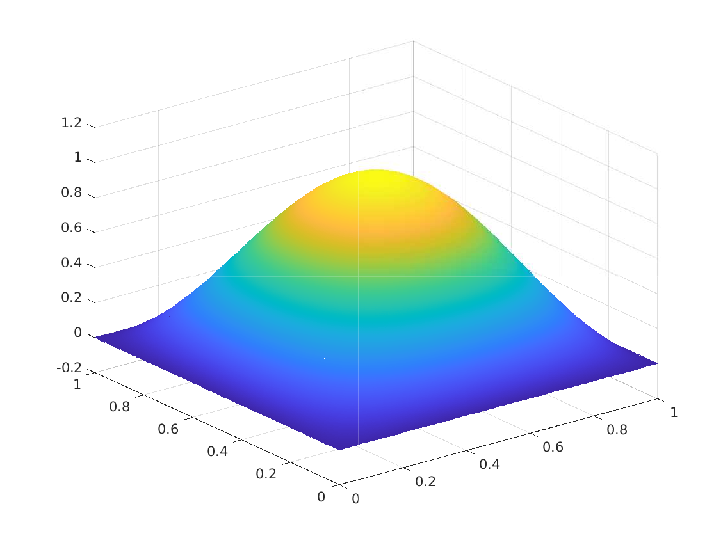
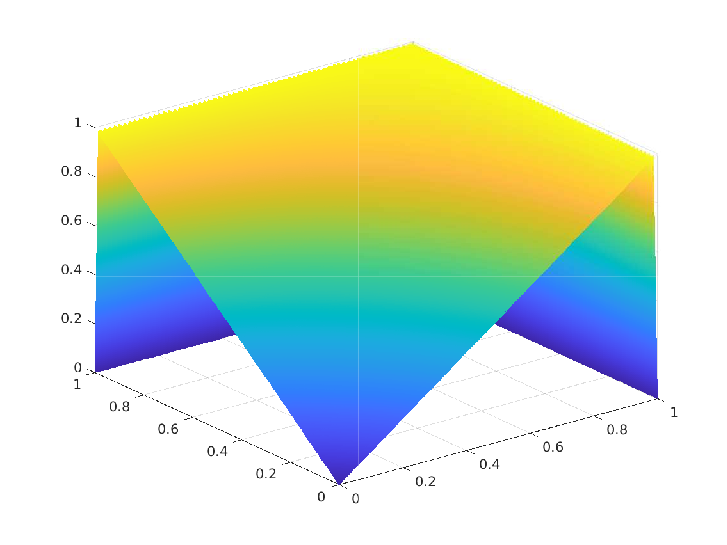exact solution for numerical experiment 2
Exact Solution
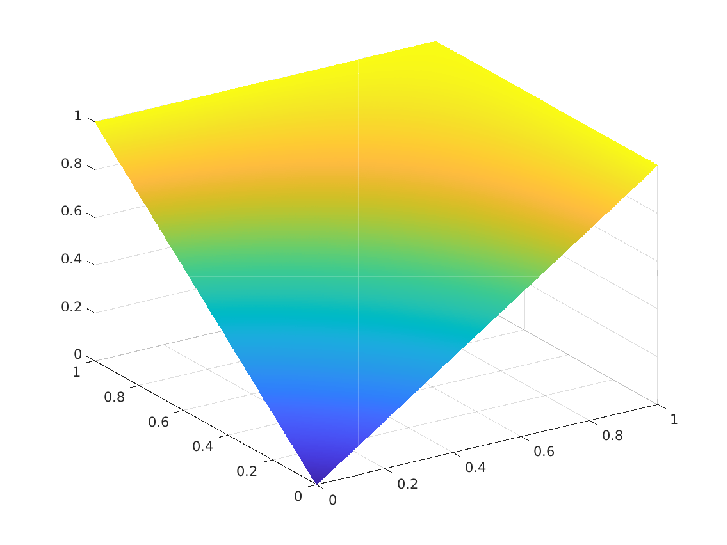numerical solution for numerical experiment 2
Numerical Solution
Read more

Elliptic optimal control problem with control constraints

We proposed a numerical scheme to reduce an elliptic optimal control problem with control constraints to a finite-dimensional optimization problem with equality and inequality-type constraints and established the order of convergence of the error as we refine the triangulation of the polygonal domain $\Omega \subset \mathbb{R}^2$. The figures below present a comparison between the exact solutions and numerical solutions from a specific numerical experiment.

Picture of exact control
Exact control
Picture of numerical control in P0 spanned space
u_h with $\mathbb{P}_0$ functions
Picture of numerical control in P1 spanned space
u_h with $\mathbb{P}_1$ functions

Picture of exact state
Exact state
Picture of numerical state in P1 spanned space
y_h with $\mathbb{P}_1$ functions
Read more

Peer-Reviewed Publications

Boyana, S. B., Lewis, T., Rapp, A., Zhang, Y. (2023). Convergence analysis of a symmetric dual-wind discontinuous Galerkin method for a parabolic variational inequality. Journal of Computational and Applied Mathematics, 422, 114922.
https://doi.org/10.1016/j.cam.2022.114922
Supported by NSF grants DMS-2111004 (PI: Y. Zhang) and DMS-2111059 (PI: T. Lewis)

Boyana, S. B., Lewis, T., Liu, S., Zhang, Y. (2024). Convergence Analysis of a Novel Discontinuous Galerkin Methods for a Convection Dominated Problem. Journal of Computers and Mathematics with Applications, Volume 175, 2024, Pages 224-235, ISSN 0898-122.
https://doi.org/10.1016/j.camwa.2024.09.027
Supported by NSF grants DMS-2111004 (PI: Y. Zhang), DMS-1929284 (PI: S. Liu) and DMS-2111059 (PI: T. Lewis)

Manuscripts in Preparation

Boyana, S. B., Lewis, T., Zhang, Y. Convergence Analysis of a Symmetric Dual-Wind Discontinuous Galerkin Methods for an Elliptic Optimal Control Problem with Control Constraints.
Supported by NSF grant DMS-2111004 (PI: Y. Zhang)